This article is based on my entry into DengAI competition on the DrivenData platform. I’ve managed to score within 0.2% (14/9069 as on 02 Jun 2020).
In this article, I assume that you’re already familiar with DengAI - EDA. You don’t have to read it to understand everything here, but it would be a lot easier if you do.
Why do we have to preprocess data?
When designing ML models we have to remember that some of them are based on the gradient method. The problem with the gradient is that it performs better on normalized/scaled data. Let me show an example:
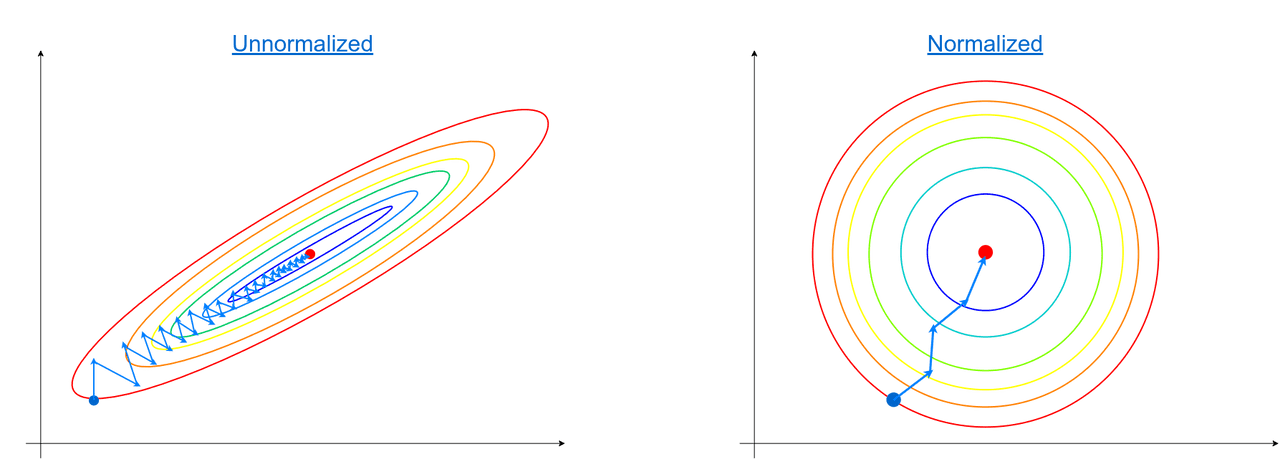
On the left side, we have a dataset that consists of two features and one of them has a larger scale than the other. In both cases, the gradient method works, but it takes a lot fewer steps to reach optimum when features lie on similar scales (right image).
What is a Normalization and what is Scaling?
Normalization
In the standard sense, normalization refers to the process of adjusting the value distribution range to fit into <-1, 1> (id doesn’t have to be exact -1 to 1 but within the same order of magnitude so the range ). Standard normalization is done by subtracting mean value from each value in the set and the dividing result by the standard deviation.
Scaling
You can see it called “min-max normalization” but scaling is another value adjustment to fit in range, but this time range is <0, 1>.
Normalization or Scaling?
There are two types of operations you can perform on the feature. You can either normalize or scale its values. Which one you choose depends on the feature itself. If you consider features that have some positive and negative values and that values are important, you should perform normalization. On the feature where negative values make no sense, you should apply scaling.
It’s not always black and white. Let’s consider a feature like a temperature. Depends on which scale you choose (Kelvin or Celsius/Fahrenheit) there might be different interpretations of what that temperature could be. Kelvin scale is an absolute thermodynamic temperature scale (starts with absolute zero and cannot go below that). On the other hand, we have scales used IRL where negative numbers are meaningful for us. When the temperature drops below 0 Celsius, water freezes. The same goes for the Fahrenheit scale, its 0 degrees describe the freezing point of the brine (concentrated solution of salt in water). The straight forward choice would be to scale Kelvins and normalize Celsius and Fahrenheit. That does not always work. We can show it on DengAI’s dataset:
| reanalysis_air_temp_k | reanalysis_avg_temp_k | reanalysis_dew_point_temp_k | reanalysis_tdtr_k | station_avg_temp_c | station_diur_temp_rng_c | station_max_temp_c | station_min_temp_c | |
|---|---|---|---|---|---|---|---|---|
| count | 1446.00 | 1446.00 | 1446.00 | 1446.00 | 1413.00 | 1413.00 | 1436.00 | 1442.00 |
| mean | 298.70 | 299.23 | 295.25 | 4.90 | 27.19 | 8.06 | 32.45 | 22.10 |
| std | 1.36 | 1.26 | 1.53 | 3.55 | 1.29 | 2.13 | 1.96 | 1.57 |
| min | 294.64 | 294.89 | 289.64 | 1.36 | 21.40 | 4.53 | 26.70 | 14.70 |
| 25% | 297.66 | 298.26 | 294.12 | 2.33 | 26.30 | 6.51 | 31.10 | 21.10 |
| 50% | 298.65 | 299.29 | 295.64 | 2.86 | 27.41 | 7.30 | 32.80 | 22.20 |
| 75% | 299.83 | 300.21 | 296.46 | 7.62 | 28.16 | 9.57 | 33.90 | 23.30 |
| max | 302.20 | 302.93 | 298.45 | 16.03 | 30.80 | 15.80 | 42.20 | 25.60 |
Some of the temperatures are on the Kelvin scale, and some on the Celsius scale. That’s not what is important here. If you look closely you should be able to group those temperatures by type:
- temperature with absolute minimum value
- temperature without absolute minimum value (can be negative)
An example of the first one is station_diur_temp_rng_c. This is something called Diurnal temperature variation and defines a variation between minimum and maximum temperature withing some period of time. That value cannot have negative values (because the difference between minimum and maximum cannot be lower than 0). That’s where we should use scaling instead of normalization.
Another example is reanalysis_air_temp_k. It is the air temperature and important feature. We cannot define a minimum value that temperature could get. If we really want there is an arbitrary minimum temperature for each city that we should never get below but that’s not what we want to do. Things like the temperature in problems like ours might have another meaning when training models. There could be some positive and negative impacts of the temperature value. In this case, it might be that temperatures below 298K positively affecting a number of cases (fewer mosquitos). That’s why we should use normalization for this one.
After checking an entire dataset we can come up with the list of features to normalize, scale and copy from our list of features:
Normalized features
'reanalysis_air_temp_k'
'reanalysis_avg_temp_k'
'reanalysis_dew_point_temp_k'
'reanalysis_max_air_temp_k'
'reanalysis_min_air_temp_k'
'station_avg_temp_c'
'station_max_temp_c'
'station_min_temp_c'Scaled features
'station_diur_temp_rng_c'
'reanalysis_tdtr_k'
'precipitation_amt_mm'
'reanalysis_precip_amt_kg_per_m2'
'reanalysis_relative_humidity_percent'
'reanalysis_sat_precip_amt_mm'
'reanalysis_specific_humidity_g_per_kg'
'station_precip_mm'
'year'
'weekofyear'Copied features
'ndvi_ne'
'ndvi_nw'
'ndvi_se'
'ndvi_sw'Why Copy?
If we look at the definition of the NDVI index, we can decide there is no reason for scalling or normalizing those values. NDVI values are already in <-1, 1> range. Sometimes we might want to copy values directly like that. Especially when original values are within the same order of magnitude as our normalized features. It might be <0,2> or <1,4>, but it shouldn’t cause a problem for the model.
The code
Now we have to write some code to preprocess our data. We’re going to use StandardScaler and MinMaxScaler from sklearn library.
import pandas as pd
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from data_info import cols_to_norm, cols_to_scale
def preproc_data(data, norm_cols=cols_to_norm, scale_cols=cols_to_scale, train_scale=None):
"""
:param data: Dataframe
:param norm_cols: List<string>
:param scale_cols: List<string>
:param train_scale: Dataframe
:return: Tuple(Dataframe, Dataframe)
"""
# Make a copy, not to modify original data
new_data = data.copy()
if train_scale is None:
train_scale = data
if norm_cols:
# Normalize temp and percipation
new_data[norm_cols] = StandardScaler().fit(train_scale[norm_cols]).transform(new_data[norm_cols])
if scale_cols:
# Scale year and week no but within (0,1)
new_data[scale_cols] = MinMaxScaler(feature_range=(0, 1)).fit(train_scale[scale_cols]).transform(
new_data[scale_cols])
return new_data, train_scaleAs an input to our function, we expect to send 3 or 4 variables. When dealing with the training set we’re sending 3 variables:
- training dataset (as pandas Dataframe)
- list of columns to normalize
- list of columns to scale
When we’re processing training data we have to define the dataset for the scaling/normalization process. This dataset is used to get values like mean or standard deviation. Because at the point of processing the training dataset we don’t have any external datasets, we’re using the training dataset. At line 19 we’re normalizing selected columns using StandardScaler():
if norm_cols:
# Normalize temp and percipation
new_data[norm_cols] = StandardScaler().fit(train_scale[norm_cols]).transform(new_data[norm_cols])StandardScaler doesn’t require any parameters when initializing, but it requires scale dataset to fit to. We could just past the new_data twice and it would work but then we need to create another preprocessing for the test dataset.
Next, we’re doing the same thing but with MinMaxScaler().
if scale_cols:
# Scale year and week no but within (0,1)
new_data[scale_cols] = MinMaxScaler(feature_range=(0, 1)).fit(train_scale[scale_cols]).transform(
new_data[scale_cols])This time we’re passing one parameter called feature_range to be sure that our scale is in range <0,1>. As in the previous example, we’re passing the scaling dataset to fit to and transform selected columns.
In the end, we’re returning transformed new_data and additionally train_scale for further preprocessing. But wait the second! What further preprocessing? Remember that we’re dealing not only with the training dataset but also with the test dataset. We have to apply the same data processing for both of them to have the same input for the model. If we would simply use preproc_data() in the same way for the test dataset, we would apply completely different normalization and scaling. The reason why is because normalization and scaling are done by the .fit() method and this method uses some given dataset to calculate mean and other required values. If you use a test dataset that might have a different range of values (there was a hot summer because of global warming etc.) your value of 28C in the test dataset will be normalized with different parameters. Let me show you an example:
Training Dataset:
Testing Dataset:
Normalizing Testing Dataset using mean and SD from the test Dataset gives us:
But if you use mean and SD from Testing dataset you’ll end up with:
You might think that the second one is better describing the dataset but that’s only true when dealing with only the testing dataset.
That’s why when building our model we have to execute it like that:
unnormalized_train_data = extract_data(path_to_train_file)
normalized_train_data, train_scale = preproc_data(unnormalized_train_data, norm_cols, scale_cols)
// Create and train model
unnormalized_test_data = extract_data(path_to_test_file)
normalized_test_data, _ = preproc_data(unnormalized_test_data, norm_cols, scale_cols, train_scale)Conclusion
We’ve just gone through a quite standard normalization process for our dataset. It is important to understand the difference between normalization and scaling. Another thing which might be even more important is feature selection for normalization (example with different temperature features), you should always try to understand your features, not only apply some hardcoded rules from the internet.
The last thing that I have to mention (and you’ve probably already thought about it) is the difference between data range in training and testing dataset. You know that normalization of the testing data should be done with the variables from training data, but shouldn’t we adjust the process to fit into a different range? Let’s say the training dataset has a temperature range between 15C and 23C and the testing dataset has range between 18C and 28C. Isn’t that a problem with our model? Actually it isn’t :) Models don’t really care about small changes like that because they are approximating continuous functions (or distributions) and unless your range differs a lot (it’s from different distribution) you shouldn’t have any issues with it.
References:
- DengAI: Predicting Disease Spread https://www.drivendata.org/competitions/44/dengai-predicting-disease-spread/